บทที่ 12 การเคลื่อนที่แบบคลื่น
Prev GENERAL PHYSICS Next

 

12.2. สมการการเคลื่อนที่ของคลื่น

ฟังก์ชัน y = f(x) แทนลักษณะของคลื่น

ถ้าแทนxด้วย(x-a)จะได้ฟังก์ชั่นไหม่คือ y = ƒ(x-a) -------------------(16)
กราฟจะไม่เปลี่ยนรูป แต่จะเลื่อนไปทางขวาเป็นระยะทาง a
ถ้าแทนxด้วย(x+a)จะได้ฟังก์ชั่นใหม่ คือ y = ƒ (x+a) ----------------(17)
กราฟจะไม่เปลี่ยนรูป แต่จะเลื่อนไปทางซ้ายเป็นระยะทาง a

 

ถ้ากราฟเคลื่อนที่ด้วยอัตราเร็ว v ภายในเวลา t จะได้ว่า
a = vt -----------------------------(18)

ดังนั้นสมการ(16)กลายเป็น        y = ƒ(x-vt) ------------------------(19)

และสมการ(17)กลายเป็น          y = ƒ(x+vt) -----------------------(20)

เมื่อเขียนสมการ(19)และ(20)รวมกัน จะได้เป็น

y(x,t) = ƒ(x±vt)--------(21)

กำหนดให้           z = x±vt----------------(22)
สมการ(21)กลายเป็น             y(x,t) = ƒ(z) -----------------------(23)

 

จากสมการ(23)สามารถหาสมการของคลื่นได้ดังนี้

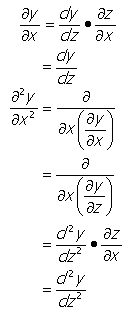
---------------------------(24)

 

 

 

 

 


----------------------------(25)

 

 


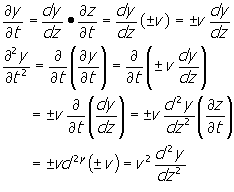
-------------------(26)

 

 

 

 

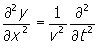ซึ่งจะได้ว่า ---------(27)

จากสมการ(25)และ(27)จะได้ว่า

-------------------------(28)

สมการ(28)เรียกว่า สมการคลื่น

รายของสมการ(28)คือ y(x,t) = ƒ1(x-vt)+ƒ1(x+vt)-----------(29)

สมการ(29)ใช้กับคลื่นรวม2คลื่นซึ่งเคลื่อนที่สวนทางกัน แต่ถ้ามีเพียงคลื่นเดียว ฟังก์ชั่นอันใดอันหนึ่งจะหายไป

ปริมาณ y(x,t) เรียกว่า ฟังก์ชั่นคลื่น(Wave Funtion)

สำหรับคลื่นรูปไซน์(Sinusoidal Wave) ฟังก์ชั่นคลื่น คือ

y(x,t) = y0sin k(x-vt) ----------------------(30)

โดยที่ y0 คือ อัมปลิจูดซึ่งมีค่าคงที่

k คือ ค่าคงที่

ถ้าแทนที่xด้วยจะได้ว่า



-----------------(31)

 

จากสมการ(31)คือ

จะได้ว่า ------------------------------(32)

หรือ -----------------------------------(33)

ค่า k เรียกว่า ค่าคงตัวของการเคลื่อนที่(Propagation Constant)หรือเลขคลื่น(Wave Number)หมายถึงจำนวนคลื่นในระยะทางหนึ่งหน่วย มีหน่วยเป็นm-1

จากสมการ(30)คือ y(x,t) = y0sin k (x-vt)

แทนค่าจากสมการ(33)ลงในสมการ(30)ได้เป็น

----------(34)

หรือ -----------(35)

หรือ -------------(36)

สำหรับคลื่นที่เคลื่อนที่ไปทางซ้าย จะได้เป็น

----------(37)

หรือ ----------(38)

หรือ -------------(39)

จากสมการ(30)คือ

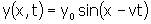
ความเร็วของอนุภาคตัวกลาง หาได้ดังนี้



--------(40)

ความเร่งของอนุภาคตัวกลาง หาได้ดังนี้


---------------(41)
---------------(42)

 

Prev Home Next
สัมประสิทธิ์ของความยืดหยุ่น   ตัวอย่างที่ 1

315 102, 315 103 ฟิสิกส์พื้นฐาน (ผศ.ณรงค์  พิศขุมทอง)

Suggestion and comment send to the WEBMASTER
Maintained and Design by Electronics Laboratory, Department of Physics, Faculty of Science,
Khonkaen University, Thailand.